Research Projects

The specific problems I have worked on so far are as follows:

• network structure inference;
• differentially private games;
• price shaping problem;
• climate-economics dynamic game.

Network Structure Inference

We investigate the capacity of an adversary to learn the underlying interaction network through repeated best response actions in linear-quadratic games. The adversary strategically perturbs the decisions of a set of action-compromised players and observes the sequential decisions of a set of action-leaked players. The central question pertains to whether such an adversary can fully reconstruct or effectively estimate the underlying interaction structure among the players.

To begin with, we establish a series of results that characterize the learnability of the interaction graph from the adversary’s perspective by drawing connections between this network learning problem in games and classical system identification theory. Subsequently, taking into account the inherent stability and sparsity constraints inherent in the network interaction structure, we propose a stable and sparse system identification framework for learning the interaction graph under both full player action observation and partial player action observation.

Some of the results is accepted by ACC2023. The complete manuscript is available on request.

Differentially Private Games

We study network games where players are involved in information aggregation processes subject to the differential privacy requirement for players’ payoff functions. We propose a Laplace linear-quadratic functional perturbation (LLQFP) mechanism, which perturbs players’ payoff functions with linear-quadratic functions whose coefficients are produced from truncated Laplace distributions.

For monotone games, we show that the LLQFP mechanism maintains the concavity property of the perturbed payoff functions, and produces a perturbed NE whose distance from the original NE is bounded and adjustable by Laplace parameter tuning. We focus on linear-quadratic games, which is a fundamental type of network games with players’ payoffs being linear-quadratic functions, and derive explicit conditions on how the LLQFP mechanism ensures differential privacy with a given privacy budget.

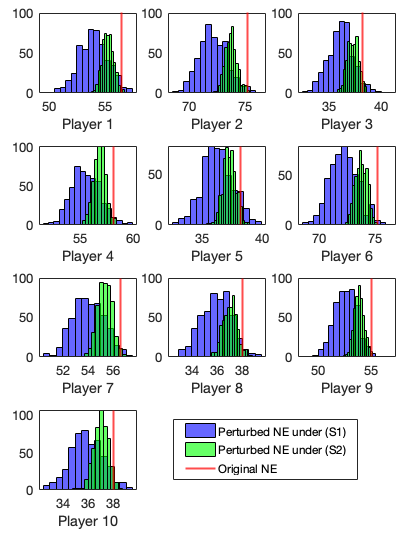
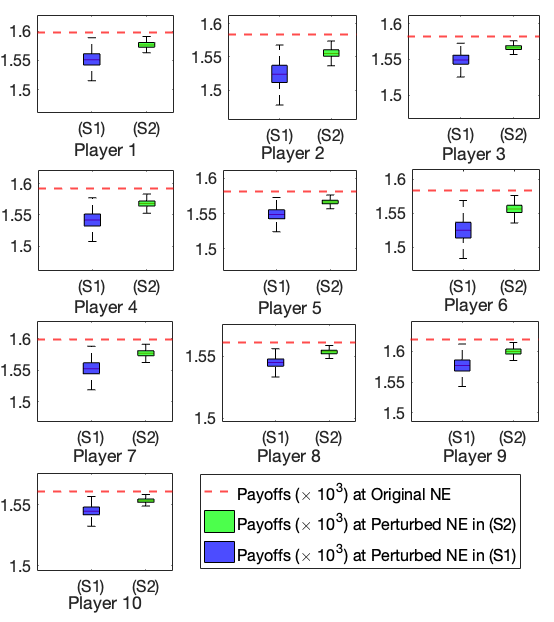
Price Shaping Problem

We study multi-agent systems with decentralized resource allocations. Agents have local demand and resource supply, and are interconnected through a network designed to support sharing of the local resource; and the network has no external resource supply. Agents decide on the consumed resource, and perhaps further the traded resource as well, to maximize their payoffs considering both the utility of the consumption, and the income from the trading. When the network supply and demand are balanced,

• a competitive equilibrium is achieved if all agents maximize their individual payoffs;
• a social welfare equilibrium is achieved if the total agent utilities are maximized.

The results are as follows:

• First, we consider multi-agent systems with static local allocations, and prove from duality theory that under general convexity assumptions, the competitive equilibrium and the social welfare equilibrium exist and agree.
• Next, we show that the agent utility functions can be prescribed in a family of socially admissible functions, under which the resource price at the competitive equilibrium is kept below a threshold.
• Further, we extend the study to dynamical multi-agent systems where agents are associated with dynamical states from linear processes, and prove that the dynamic competitive equilibrium and the dynamic social welfare equilibrium continue to exist and coincide with each other.
• Finally, we present a recursive representation of the competitive equilibriums using dynamic programming, and a receding horizon approach for smoothing the dynamic pricing as a dynamic competitive equilibrium social shaping method.

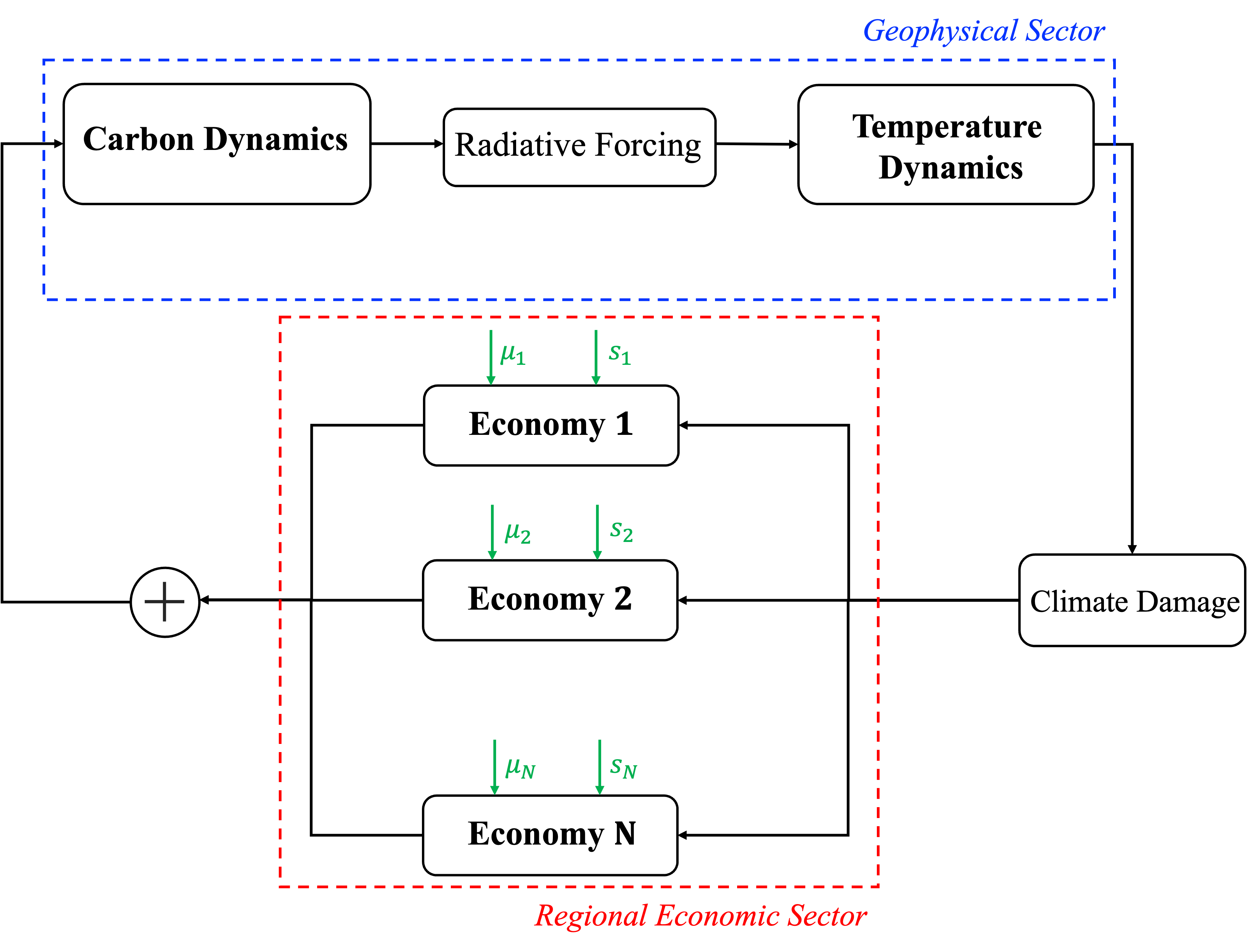
Climate-Economics Dynamic Game

One of the most widely used models for studying the geographical economics of climate change is the Regional Integrated model of Climate and the Economy (RICE). We investigate how cooperation and competition arise in regional climate policies under the RICE framework from the standpoints of game theory and optimal control.

First, we show that the RICE model is inherently a dynamic game. Second, we study both cooperative and non-cooperative solutions to this RICE dynamic game.

• Cooperative settings:
  • We investigate the global social welfare equilibrium that maximizes the weighted and cumulative social welfare across regions.
  • We divide the regions into two clusters: developed and developing, and look at the social welfare frontier under the notion of Pareto optimality.
  • We present a receding horizon approach to approximate the global social welfare equilibrium for robustness and computational efficiency.
• Non-cooperative settings:
  • We study best-response dynamics and open-loop Nash equilibrium of the RICE game. A Recursive Best-response Algorithm for Dynamic Games (RBA-DG) is proposed to describe the sequences of best-response decisions for dynamic games, which indicates convergence to open-loop Nash equilibrium when applied to the RICE game by numerical studies.
  • We also study online receding horizon feedback decisions of the RICE game. A Receding Horizon Feedback Algorithm for Dynamic Games (RHFA-DG) is proposed.

The results reveal how game theory may be used to facilitate international negotiations towards consensus on regional climate-change mitigation policies, as well as how cooperative and competitive regional relations shape climate change for our future. All these proposed solution concepts are implemented and open sourced using the latest updated parameters and data at https://github.com/chyj528/RICE-GAME.